There is a curious phenomenon in geometric topology: some problems seem to get easier as you increase the dimension you’re looking at. The catchphrase is that “high dimensional topology is easy because you have more room to move around” – let’s see what this means.
The -dimensional topological (resp. smooth) Poincaré conjecture says that if a closed
-manifold is homotopy equivalent to
, then it is homeomorphic (resp. diffeomorphic) to
.
The most well-known of this web of conjectures is the 3-dimensional topological case, which is equivalent to: “A simply connected closed 3-manifold must be homeomorphic to .” This was famously resolved by Perelman in the early 2000s. The 4-dimensional topological Poincaré conjecture was proved by Freedman in 1982; and for
, the n-dimensional topological Poincaré conjecture was proved in the mid-60s. We are, in some sense, going backwards in difficulty! (Rest assured, though, that the 2- and 1-dimensional cases are not so terrible that they won’t be solved in the millenium; they were known in the early 20th century. 3 is the first dimension which is complicated enough for these sorts of problems to be interesting.)
Because we know the topological Poincaré conjecture is true in all dimensions, we can reformulate the smooth Poincaré conjecture as follows: if a smooth manifold is homeomorphic to
, is
necessarily diffeomorphic to
?
The question of determining the number of diffeomorphism classes of smooth manifolds that are homeomorphic to is known as the exotic spheres problem. (Such a smooth manifold – one homeomorphic, but not diffeomorphic, to
– is called an exotic sphere.) The following table shows how many exotic spheres there are in each dimension
.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 1 | 1 | ??? | 1 | 1 | 28 | 2 | 8 | 6 | 992 | 1 |
While the 28 or 992 might seem mysterious, it’s less so than one might imagine – the exotic spheres problem, in dimensions above 5, has been essentially reduced to a fundamental (yet very difficult!) question in algebraic topology; more on this later. Worth noting is that dimension 3 was solved by Moise in 1952, and the 4-dimensional case is completely open; experts are not even entirely certain whether or not to believe it’s true.
So there is, fundamentally, some sort of difference between low-dimensional topology and high-dimensional topology. Why?
Everything is because of the h-cobordism theorem.
A cobordism between two closed –manifolds
and
is a compact
-manifold
whose boundary is the disjoint union of
and
. Note that we need
to be compact for this to be an interesting notion; otherwise a cobordism between any pair of closed manifolds
is given by
.
Some canonical examples are given by a pair of pants, a cobordism between and
; the solid torus, a cobordism between the torus and the empty set; and for any manifold
,
is a cobordism between
and itself.
An h-cobordism between two closed -manifolds
and
is a cobordism
such that the inclusions
,
are homotopy equivalences. An example is, as above, given by
, an h-cobordism between
and itself. Giving you more examples will be problematic, because:
h-cobordism theorem (Smale): Let be a topological (resp. smooth) h-cobordism, and suppose
and
be simply connected. If, in addition,
, then
is homeomorphic (resp. diffeomorphic) to
. In particular,
is homeomorphic (resp. diffeomorphic) to
.
I still find this theorem absolutely astonishing. It is such an immensely powerful result from what don’t appear to be very strong conditions. (In fact, it’s still true topologically in low dimensions; Freedman’s proof of the 4-dimensional topological Poincaré conjecture starts by proving the topological 4-dimensional h-cobordism theorem; and the 3-dimensional h-cobordism theorem is now known to be true thanks to the 3-dimensional Poincaré conjecture. Perhaps part of what makes 4 dimensional topology so weird is that the smooth 4-dimensional h-cobordism theorem is absolutely, irrevocably, false. Not unknown, but false.)
Why does this fascinating, but seemingly unrelated statement help us? Well…
Corollary: If is a closed manifold, homotopy equivalent to
,
, then
is homeomorphic to
.
Proof: Embed two small closed balls into
, whose images are disjoint, and delete their interiors. Call the resulting manifold
. Some algebra shows that
is an h-cobordism between the two boundary copies of
; so that
is homeomorphic to
. We want to extend this to a homeomorphism
; it suffices to show that given a homeomorphism
, we can extend this to a homeomorphism
. The process of doing so is known as Alexander’s trick; if
is written in polar coordinates, simply write
; the idea being that we’re repeating
“levelwise” until we get to 0, which we fix. One can check that this is continuous. Even if
was smooth, this
is rarely smooth at the origin, which is why we haven’t simultaneously proved the smooth high-dimensional Poincaré conjecture (which, as above, is false). Indeed, there are many diffeomorphisms
which cannot be extended to a diffeomorphism of the disc.
(As a side note, the proof of the 5-dimensional Poincaré conjecture is slightly different; this was achieved, instead of deleting small balls, by showing that any closed 5-manifold, homotopy equivalent to , must be h-cobordant to it.)
As for the exotic spheres problem, this helps us too. h-cobordisms are somehow more ‘algebraically assailable’ than diffeomorphisms; Milnor was able to write down a few exact sequences that help us with our problem.
In the following, is the group of h-cobordism classes of
-manifolds homeomorphic to
; the group operation is connected sum, though we won’t prove this actually gives you a group.
is the group of h-cobordism classes of
-manifolds homeomorphic to
that bound parallelizable manifolds. While this sounds complicated, it’s not that hard (for Milnor) to understand this group; it’s cyclic, and we know its order in all dimensions.
is the
th stable homotopy group of spheres, and
is a certain (again, understood) subgroup; we know its order.
Milnor finds exact sequences, for ,
; and for
, we get the slightly more ugly sequence
The map
is known as the Kervaire invariant; it was known in the 60s that it could only be nonzero for
of the form
; recent work by Hill, Hopkins, and Ravenel shows that it is zero for all
. It is known to be nonzero for
, and it’s unknown for
. Dimensions close to these numbers are special; the order of
is known in every dimension
, and
in these dimensions iff
. As a result of the above, except in dimensions 125 and 126, the order of
is known as a function of the order of
. The calculation of this group,
, is one of the main motivating problems of homotopy theory, and is a major open problem. Nonetheless, it is expected that in dimension large enough, the smooth Poincaré conjecture is false.
How the h-cobordism theorem helps us here is obvious: the group is, as a result, isomorphic to the group of diffeomorphism classes of exotic spheres! So the above is entirely about exotic spheres, except in dimension
, where all exotic spheres are h-cobordant; but we have absolutely no idea whether or not they’re diffeomorphic.
Hopefully this convinces you that the h-cobordism theorem (or things related to it) is what causes this ‘high-dimensional simplicity’; but why is it true, and where does that catchphrase, “there’s more room to move around”, come from? Certainly the h-cobordism theorem doesn’t sound like this. So, next time: why the h-cobordism theorem is true, and how it relates to having extra wiggle room.

Hey Mike–a couple of questions
1) In the statement of the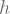 -cobordism theorem, you say that
-cobordism theorem, you say that ![W\cong M\times [0,1]](https://s0.wp.com/latex.php?latex=W%5Ccong+M%5Ctimes+%5B0%2C1%5D&bg=ffffff&fg=666666&s=1&c=20201002) (what the hell symbol do topologists use for homeomorphism?). Can you actually assume that there is a homeomorphism
(what the hell symbol do topologists use for homeomorphism?). Can you actually assume that there is a homeomorphism ![W\to M\times [0,1]](https://s0.wp.com/latex.php?latex=W%5Cto+M%5Ctimes+%5B0%2C1%5D&bg=ffffff&fg=666666&s=1&c=20201002) compatible with the obvious mapping
compatible with the obvious mapping ![M\to M\times [0,1]](https://s0.wp.com/latex.php?latex=M%5Cto+M%5Ctimes+%5B0%2C1%5D&bg=ffffff&fg=666666&s=1&c=20201002) (e.g. putting it in the
(e.g. putting it in the  slice)?
slice)?
2) In the proof of the corollary, the statement ‘some algebra shows’ seems very vague. Perhaps I am just nitpicking on the phrase ‘algebra’, but is it hard to show that it really is an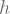 -cobordism?
-cobordism?
3) As an outsider, much of the above seems like a ‘trick’. Namely, people noticed that this notion of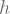 -cobordism was both restrictive, and easy to ‘make appear’ on homotopy spheres. Is there an intuition why one would consider such an object? Being topology, I would imagine that there is a very clear topological picture as to
-cobordism was both restrictive, and easy to ‘make appear’ on homotopy spheres. Is there an intuition why one would consider such an object? Being topology, I would imagine that there is a very clear topological picture as to
a) Why this is an obvious thing to consider
and
b) What it’s really doing in the proof.
Thanks!
LikeLike
Usually, one is sticking with either homeomorphism or diffeomorphism, and if the other word shows up, one just says words. And in these cases, we just write $\cong$.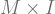 with a ton of other stuff on it, let’s get rid of all that other stuff.”
with a ton of other stuff on it, let’s get rid of all that other stuff.”
Yes! You’re right that this is a thing we can do. This is going to show up in the proof, too, which basically goes like “Well we know we can write it as
To actually show this is an h-cobordism, apply Mayer-Vietoris once to see that deleting one ball gives you something with trivial homology, and apply it again to see that the inclusion of the second sphere induces an isomorphism on homology. The fundamental group of a manifold of dimension at least 3 doesn’t change when you puncture it, so our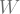 is simply connected, so a version of Whitehead promises us that these inclusions are a homotopy equivalence.
is simply connected, so a version of Whitehead promises us that these inclusions are a homotopy equivalence.
Regarding h-cob’s appearance: historically, I think, it really was a trick. Thom apparently invented the notion for some reason I don’t know, and Milnor worked with it a bit to see calculate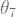 and
and 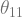 in “Differentiable Manifolds which are Spheres”. But even then he expected that all h-cobordant manifolds are diffeomorphic. (This is false, and he was hoping for too much – one really needs the simply connected condition.) Side note: I find it interesting that this is what he suggests and not that the more general fact that the cobordism is a cylinder. The view I have of the trick is really just that these h-cobordisms actually do seem accessible – and are easier to construct than diffeomorphisms, provided you have some decent reason to believe your manifolds are the same. (The way Freedman’s classification of simply connected 4-manifolds worked was to start with two s.c. 4-manifolds with the same intersection form, and use this to actually write down an h-cobordism, provided your two manifolds also had the same Kirby-Seibenmann invariant, a
in “Differentiable Manifolds which are Spheres”. But even then he expected that all h-cobordant manifolds are diffeomorphic. (This is false, and he was hoping for too much – one really needs the simply connected condition.) Side note: I find it interesting that this is what he suggests and not that the more general fact that the cobordism is a cylinder. The view I have of the trick is really just that these h-cobordisms actually do seem accessible – and are easier to construct than diffeomorphisms, provided you have some decent reason to believe your manifolds are the same. (The way Freedman’s classification of simply connected 4-manifolds worked was to start with two s.c. 4-manifolds with the same intersection form, and use this to actually write down an h-cobordism, provided your two manifolds also had the same Kirby-Seibenmann invariant, a 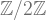 -valued invariant that shows up in the construction.) So, much like formal group laws can be considered a stepping stone between Lie groups and their Lie algebras, one might think of h-cobordisms as a stepping stone between the differential topology of your manifolds and the algebra/homotopy.
-valued invariant that shows up in the construction.) So, much like formal group laws can be considered a stepping stone between Lie groups and their Lie algebras, one might think of h-cobordisms as a stepping stone between the differential topology of your manifolds and the algebra/homotopy.
LikeLike